Letra griega "pi" es una constante en geometría euclidiana.. Símbolo adoptado en 1706 por William Jones y popularizado por Leonhard Euler.
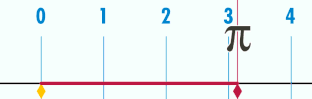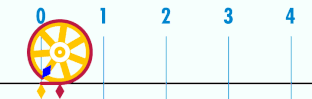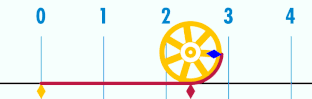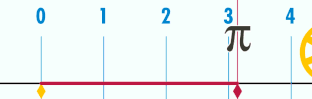
"pi" es la relación entre la longitud de una circunferencia y su diámetro.
Euclides fue el primero en demostrar que la relación entre una circunferencia y su diámetro es una cantidad constante.
y un círculo de radio . El área del círculo es 
.La ecuación sobre los números complejos
admite una infinidad de soluciones reales positivas, la más pequeña de las cuales es precisamente 
(véase identidad de Euler). 
Algunas aproximaciones históricas de valores de π, anteriores a la época computacional, se muestran en la siguiente tabla:
| Año | Matemático o documento | Cultura | Aproximación | Error
(en partes por millón) |
| ~1900 a. C. | Papiro de Ahmes | Egipcia | 28/34 ~ 3,1605 | 6016 ppm |
| ~1600 a. C. | Tablilla de Susa | Babilónica | 25/8 = 3,125 | 5282 ppm |
| ~600 a. C. | La Biblia (Reyes I, 7,23) | Judía | 3 | 45 070 ppm |
| ~500 a. C. | Bandhayana | India | 3,09 | 16 422 ppm |
| ~250 a. C. | Arquímedes de Siracusa | Griega | entre 3 10/71 y 3 1/7 empleó 211875/67441 ~ 3,14163 |
<402 ppm 13,45 ppm |
| ~150 | Claudio Ptolomeo | Greco-egipcia | 377/120 = 3,141666... | 23,56 ppm |
| 263 | Liu Hui | China | 3,14159 | 0,84 ppm |
| 263 | Wang Fan | China | 157/50 = 3,14 | 507 ppm |
| ~300 | Chang Hong | China | 101/2 ~ 3,1623 | 6584 ppm |
| ~500 | Zu Chongzhi | China | entre 3,1415926 y 3,1415929 empleó 355/113 ~ 3,1415929 |
<0,078 ppm 0,085 ppm |
| ~500 | Aryabhata | India | 3,1416 | 2,34 ppm |
| ~600 | Brahmagupta | India | 101/2 ~ 3,1623 | 6584 ppm |
| ~800 | Al-Juarismi | Persa | 3,1416 | 2,34 ppm |
| 1220 | Fibonacci | Italiana | 3,141818 | 72,73 ppm |
| 1400 | Madhava | India | 3,14159265359 | 0,085 ppm |
| 1424 | Al-Kashi | Persa | 2π = 6,2831853071795865 | 0,1 ppm |
A pesar de tratarse de un número irracional continúa siendo averiguada la máxima cantidad posible de decimales. Los cincuenta primeros son:
Si en este poema cuentas las letras de cada palabra tendrás las primeras veinte cifras de pi :
“Soy y seré a todos definible,
mi nombre tengo que daros,
cociente diametral siempre inmedible
soy de los redondos aros"
Desde el diseño de la primera computadora se empezaron a desarrollar programas para el cálculo del número π con la mayor cantidad de cifras posible. De esta forma, en 1949 un ENIAC fue capaz de romper todos los récords, obteniendo 2037 cifras decimales en 70 horas. Poco a poco fueron surgiendo ordenadores que batían récords y, de esta forma, pocos años después (1954) un NORAC llegó a 3092 cifras. Durante casi toda la década de los años 1960 los IBM fueron batiendo récords, hasta que un IBM 7030 pudo llegar en 1966 a 250.000 cifras decimales (en 8 h y 23 min). Durante esta época se probaban las nuevas computadoras con algoritmos para la generación de series de números procedentes de π.
En la década de 2000, los ordenadores son capaces de obtener números que poseen una inmensa cantidad de decimales. En 2009 se hallaron más de dos billones y medio de decimales de pi mediante el uso de una supercomputadora T2K Tsukuba System, compuesta por 640 computadoras de alto rendimiento, que juntas consiguen velocidades de procesamiento de 95 teraflops. Lo obtuvieron en 73 horas y 36 minutos.
| Año | Descubridor | Ordenador utilizado | Número de cifras decimales |
| 1949 | G.W. Reitwiesner y otros15 | ENIAC | 2037 |
| 1954 | NORAC | 3092 | |
| 1959 | Guilloud | IBM 704 | 16 167 |
| 1967 | CDC 6600 | 500 000 | |
| 1973 | Guillord y Bouyer15 | CDC 7600 | 1 001 250 |
| 1981 | Miyoshi y Kanada15 | FACOM M-200 | 2 000 036 |
| 1982 | Guilloud | 2 000 050 | |
| 1986 | Bailey | CRAY-2 | 29 360 111 |
| 1986 | Kanada y Tamura15 | HITAC S-810/20 | 67 108 839 |
| 1987 | Kanada, Tamura, Kobo y otros | NEC SX-2 | 134 217 700 |
| 1988 | Kanada y Tamura | Hitachi S-820 | 201 326 000 |
| 1989 | Hermanos Chudnovsky | CRAY-2 y IBM-3090/VF | 480 000 000 |
| 1989 | Hermanos Chudnovsky | IBM 3090 | 1 011 196 691 |
| 1991 | Hermanos Chudnovsky | 2 260 000 000 | |
| 1994 | Hermanos Chudnovsky | 4 044 000 000 | |
| 1995 | Kanada y Takahashi | HITAC S-3800/480 | 6 442 450 000 |
| 1997 | Kanada y Takahashi | Hitachi SR2201 | 51 539 600 000 |
| 1999 | Kanada y Takahashi | Hitachi SR8000 | 68 719 470 000 |
| 1999 | Kanada y Takahashi | Hitachi SR8000 | 206 158 430 000 |
| 2002 | Kanada y otros15 [3] | Hitachi SR8000/MP | 1 241 100 000 000 |
| 2004 | Hitachi | 1 351 100 000 000 | |
| 2009 | Daisuke Takahashi16 | T2K Tsukuba System | 2 576 980 370 000 |
| 2009 | Fabrice Bellard17 | Core i7 CPU, 2.93 GHz; RAM: 6GiB | 2 699 999 990 000 |
| 2010 | Shigeru Kondo | 2 x Intel Xeon X5680, 3.33 GHz | 5 000 000 000 000 |
| 2011 | Shigeru Kondo | 10 000 000 000 000 |
Según determinadas coincidencias numéricas, los Días de Aproximación a Pi son:
- 14 de marzo (3/14 en formato de fecha inglés)
- 26 de abril
- 22 de julio (22/7 que es una aproximación de pi)
- 10 de noviembre (es el 314º día del calendario gregoriano)
- 21 de diciembre (es el día 355, en referencia a la aproximación 355/113)
¿Cuál es el animal que tiene entre 3 y 4 ojos?
El Pi - ojo
El
número Pi
El
número Pi es digno de admiración
tres
coma uno
cuatro
uno
todas
sus cifras siguientes también son iniciales
cinco
nueve
dos,
porque nunca se termina.
No
permite abarcarlo con la mirada
seis cinco
tres
cinco
con
un cálculo
ocho nueve
con
la imaginación
siete nueve
o
en broma tres
dos tres,
es decir, por comparación
cuatro
seis
con cualquier otra cosa
dos
seis
cuatro tres
en
el mundo.
La
más larga serpiente después de varios metros se interrumpe
Igualmente,
aunque un poco más tarde, hacen las serpientes fabulosas.
El
cortejo de cifras que forman el número Pi
no
se detiene en el margen de un folio,
es
capaz de prolongarse por la mesa, a través del aire,
a
través del muro, de una hoja, del nido de un pájaro,
de
las nubes, directamente al cielo
a
través de la total hinchazón e inmensidad del cielo.
¡Oh
qué corta es la cola del cometa, como la de un ratón!
¡Qué
frágil el rayo de la estrella que se encorva en cualquier espacio!
Pero
aquí dos
tres
quince trescientos
noventa
mi
número de teléfono la talla de tu camisa
año
mil novecientos setenta y tres sexto piso
número
de habitantes sesenta y cinco décimos
la
medida de la cadera dos dedos la charada y el código
en
la que mi ruiseñor vuela y canta
y
pide un comportamiento tranquilo
también
transcurren la tierra y el cielo
pero
no el número Pi, éste no,
él
es todavía un buen cinco
no
es un ocho
cualquiera
ni
el último
siete
metiendo
prisa, oh, metiendo prisa a la perezosa eternidad
para
la permanencia.
Wislawa
Szymborska
(Premio Nobel de Literatura 1996)
